Experimental Study on the Evolution of Dynamic Pore Pressure and Unidirectional and Bidirectional Vibrations of Phosphogypsum

1 Introduction

Phosphogypsum (PG) is a by-product of the production process of wet phosphoric acid. In recent years, the market demand for phosphorus compound fertilizer has been increasing, and the emission of PG has also been increasing (Cao et al., 2021). However, the utilization rate of PG is less than 40%, a large number of unused PG piles on the ground form PG dams, and the worldwide stockpile has reached six billion tons (Zhang et al., 2019). Phosphogypsum ponds are necessary production facilities for phosphate mines and phosphorus chemical industries and are also one of the major sources of danger. Wet PG ponds are tailings ponds. Among the various factors leading to tailings pond accidents, earthquakes are the second most important factor after heavy rainfall (Rico et al., 2008). Some of the PG ponds in operation in China are located in high-intensity seismic regions (Mi et al., 2015). Once the dams are destabilized, they will have catastrophic consequences for the downstream areas of the dams (Wang et al., 2021; Zheng et al., 2022). The former State Administration of Work Safety of China (now merged into the Ministry of Emergency Management of the People’s Republic of China, 2016) issued Safety technical regulation on phosphogypsum stack (AQ 2059-2016), and explicitly stipulated that the design of PG ponds must meet the dynamic stability requirements.

The current research on PG mainly focuses on comprehensive utilization, and there is little research on the physical and mechanical properties and other aspects of PG. Xu et al. (2008) found that PG had strong shear strength and good water stability. Shen et al. (2008) found that PG had a plate-like crystal structure, a liquid-plastic limit similar to that of powdered soil, good permeability, and unique compression and consolidation characteristics. Tayibi et al. (2009) found that the solubility of PG had a strong relationship with PH value and found that most of the particles had rhombic or monoclinic crystal structures using scanning electron microscopy. Zhang et al. (2007) studied the relationship between the solubility of PG and temperature and found that PG had obvious shear expansion characteristics in a consolidated undrained test. Mi et al. (2015) found that deposited PG had obvious anisotropy, a high friction angle, and anti-liquefaction ability. Lu et al. (2021) divided the stress-strain curve of typical PG in a triaxial shear test into three stages and summarized the dynamic parameters, such as dynamic strength, dynamic shear modulus, and damping ratio of PG, and their variation laws by a dynamic triaxial test.

Many scholars have studied the dynamic properties of rock and soil under cyclic action and achieved a lot of results (You et al., 2021; Zhou et al., 2022). Seed et al. (1966) proposed to express the relationship between the pore pressure ratio and the loading period ratio by the inverse sine trigonometric function through a dynamic triaxial test of saturated sandy soil, providing a theoretical basis for the subsequent research on the development law of the dynamic pore pressure of soil. Zhang et al. (2006) modified the Seed pore pressure model and proposed the dynamic pore pressure prediction formula applicable to tailing materials. Wang et al. (2012) conducted dynamic triaxial tests on lime-treated expansive soil with different confining pressures, vibration frequencies, consolidation ratios, and cycle numbers to discuss the dynamic properties of lime-treated expansive soil. Du et al. (2016) studied the pore pressure growth characteristics of tailing soils under cyclic loading, proposed their pore pressure growth model, and pointed out that the model was also applicable to sandy soils. Zhang et al. (2018) studied the evolution law of dynamic pore pressure of tailings under different consolidation conditions, indicated the obvious stages in the evolution of dynamic pore pressure of tailings, and deduced the critical pore water pressure equations under isostatic consolidation and anisotropic consolidation based on the limit equilibrium theory.

In the previous analyses of seismic responses, the seismic action was considered to be dominated by horizontal shear, so the unidirectional vibration cyclic load was used to simulate the seismic motion (Seed et al., 1971). In the near-field seismic action, the effect of vertical seismic force is not negligible, so using bidirectional vibrations to simulate the seismic action is more practical. In recent years, many scholars have studied the dynamic properties of soil under bidirectional vibrations. Rascol (2009) studied the coupled stress paths of dynamic spherical stress and dynamic partial stress with bidirectional vibrations under undrained conditions of saturated sandy soil. They found that the dynamic pore pressure and dynamic modulus of soil change with the amplitude of dynamic spherical stress and phase difference. Idriss et al. (1978) proposed the softening index and established the expression between the softening index and the number of cycles. Wang et al. (2009) found that the increase in cyclic partial stress and radial cyclic stress could accelerate the softening of soil when the saturated soft clay soil was under bidirectional vibrations. Xie et al. (2017) conducted multiple sets of unidirectional and bidirectional vibration tests on saturated clay and found that the accumulated plastic strain of specimens developed faster under unidirectional vibrations at the same stress level. Liu et al. (2021) found obvious phases in developing the accumulated pore pressure of saturated tailing sand under high-stress conditions and preliminarily established the dynamic pore pressure growth model of tailing silt under unidirectional and bidirectional vibrations.

Due to the limitation of test apparatuses and other reasons, there are few reports on the research of dynamic characteristics of PG under unidirectional and bidirectional vibrations. In this article, the KTL-DYN10 bidirectional dynamic triaxial apparatus (Qiankunxing Intelligent Technology Company, Qingdao, China) was used to conduct dynamic triaxial tests on PG under different consolidation and vibration conditions to explore the dynamic strength change law and damage mechanism of PG under different cyclic vibration conditions and provide a design basis for the seismic stability of PG dams.

2 Experimental Content and Methods

2.1 Test Equipment

In the test, KTL-DYN10 bidirectional dynamic triaxial apparatus was applied, as shown in Figure 1. The hardware system includes axial loading equipment, a dynamic confining pressure controller, a backpressure controller, a pressure chamber, an eight-channel dynamic controller, and data acquisition equipment. The software system is a DSP high-speed digital control system with a maximum operating frequency of up to 50 Hz and a maximum dynamic stress amplitude of up to ±10 kN. Figure 2 shows the time-history curves of axial and radial loads measured simultaneously when the dynamic load is 100 kPa. It can be seen from the figure that the axial and radial loads are stable, indicating that the apparatus has good performance and the test results are credible.

FIGURE 1. KTL-DYN10 bidirectional dynamic triaxial apparatus.

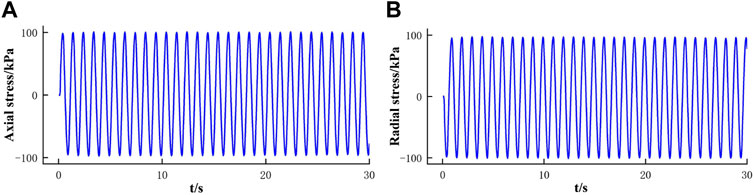
FIGURE 2. Time–history curves measured under bidirectional vibrations: (A) Time–history curves of axial stress; (B) time–history curves of radial stress.

2.2 Test Soil Sample and Test Preparation

The PG used in this experiment was taken from a PG pond discharged from a group in Yunnan after producing phosphoric acid. The PG is dark gray. Its chemical components are shown in Table 1, and its main component is gypsum dihydrate. The measuring results of the test show that the liquid limit of PG is 26.8%, the plastic limit is 18.4%, and the plasticity index is 8.4. The diameters of its particles are mainly between 0.005 and 0.075 mm, closer to that of pulverized soil, and the cumulative curve is shown in Figure 3. The inhomogeneity coefficient Cu is 3.45, and the curvature coefficient Cc is 1.52. The above analyses show that the PG has a concentrated particle size, a narrow distribution range, and good uniformity, which is not conducive to the stability of the tailings ponds.

TABLE 1. Chemical components of PG/%.

FIGURE 3. Cumulative curve of the particle size distribution of PG.

The main component of PG is gypsum dihydrate. When the temperature exceeds 60°C, dihydrate gypsum starts to dehydrate and becomes hemihydrate gypsum or anhydrous gypsum, as shown in Eq. 1:

Therefore, in the process of specimen preparation, to avoid losing crystal water during drying, according to the China national standard Phosphogypsum (Global, 2018), the drying temperature of PG is suggested to be 40 ± 2°C. In the test, cylindrical specimens with a diameter of 50 mm and a height of 105 mm that were compacted in four layers were used, as shown in Figure 4. According to the deposition law in most PG dams, the dry densities of the samples were determined to be 1.12 g/cm³.

FIGURE 4. Test sample.

2.3 Test Scheme

Under unidirectional vibrations, $CSR={\sigma }_d/\mathbf{2}{\sigma }_{\mathbf{0}}^{\prime }$. Under bidirectional vibrations, $CSR={\sigma }_d/{\sigma }_{\mathbf{0}}^{\prime }$. Under the same CSR conditions, cyclic dynamic stress of ${\sigma }_d$ was applied in the axial direction under unidirectional vibrations, and cyclic dynamic stress of ${\sigma }_d/\mathbf{2}$ was applied in the radial and axial directions under bidirectional vibrations. A sine wave was chosen for the test, the vibration frequency was 1 Hz, and the phase angle was set to $\mathbf{180}°$ for bidirectional vibrations. The pore pressure reaching 95% of the consolidation confining pressure during the liquefaction was used as the damage standard of PG. After the specimens were prepared, they were saturated with CO₂, distilled water, and back pressure to increase the saturation of the specimens. When the saturation reached 97% (B > 0.97), the consolidation was carried out under the corresponding conditions, and the dynamic load was applied after the consolidation was completed.

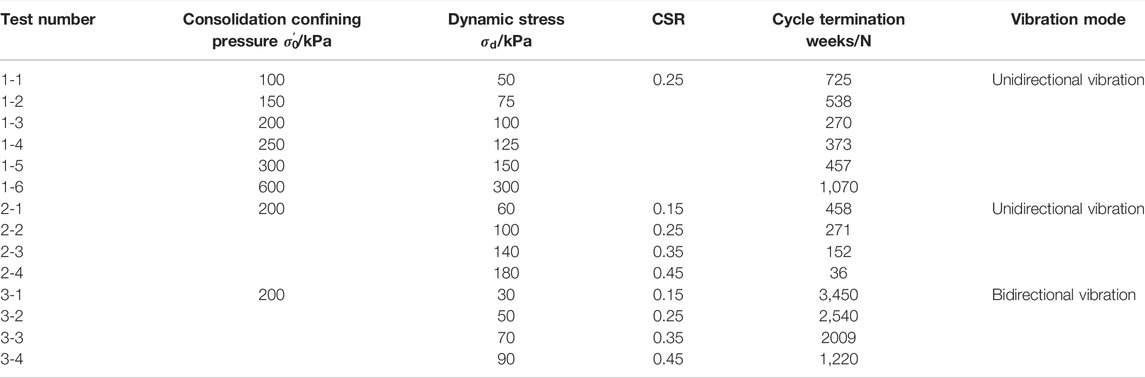
Fourteen sets of valid test data were obtained. Six groups of tests were designed under the same CSR conditions with unidirectional vibrations, and the consolidation-confining pressure and dynamic stress were gradually increased. The other eight groups of tests were performed under the same consolidation confining pressure, and the CSR was continuously increased under unidirectional and bidirectional vibrations. The specific test scheme is shown in Table 2.

TABLE 2. Test scheme.

3 Test Results and Analysis

3.1 Pore Pressure Growth Characteristics of PG Under Unidirectional and Bidirectional Vibrations

Under seismic action, PG dams have the risk of liquefaction and instability. Their evolution law of pore pressure can reflect their liquefaction process. Therefore, it is necessary to analyze the development law of pore pressure when studying the dynamic characteristics of PG under unidirectional and bidirectional vibrations.

The thickness of the development curves of instantaneous pore pressure indicates the difference between the maximum and minimum pore pressure in this vibration cycle, which is related to the dynamic strength of the specimens and the applied dynamic stress. Figure 5 shows the growth curves of instantaneous pore pressure of typical PG under unidirectional and bidirectional vibrations, vibration number ratio is the ratio of current vibration times to pore pressure corresponding to liquefaction, and pore pressure ratio is the ratio of current pore pressure to consolidation confining pressure. Under the same conditions, cyclic dynamic stress of ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ was applied in the axial direction under unidirectional vibrations, and cyclic dynamic stress of ${\mathit{\text{σ}}}_{\mathit{\text{d}}}/\mathbf{2}$ was applied in the radial and axial directions under bidirectional vibrations. The axial and radial dynamic stresses are equal in size and opposite in direction, and the phase angle is 180°. So the dynamic stress applied under unidirectional vibrations is two times that under bidirectional vibrations, and the thickness of the curves of the instantaneous pore pressure under unidirectional vibrations is significantly greater than that under bidirectional vibrations.

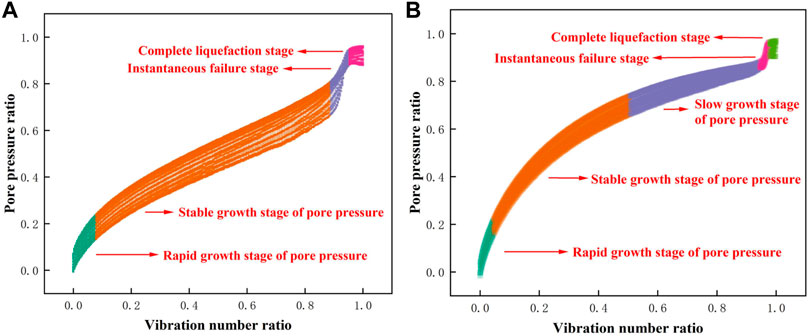
FIGURE 5. Development curves of instantaneous pore pressure of typical PG: (A) unidirectional vibrations; (B) bidirectional vibrations.

According to the growth curve of instantaneous pore pressure and the range of pore pressure ratio, under unidirectional vibrations, the liquefaction process of PG can be divided into four stages (Figure 5A): the rapid growth stage of pore pressure (pore pressure ratio between 0 and 0.2), the stable growth stage of pore pressure (pore pressure ratio between 0.2 and 0.7), the instantaneous failure stage (pore pressure ratio between 0.7 and 0.9), and the complete liquefaction stage (pore pressure ratio between 0.9 and 1.0). Under bidirectional vibrations, the liquefaction process can be divided into five stages (Figure 5B): the rapid growth stage of pore pressure (pore pressure ratio between 0 and 0.2), the stable growth stage of pore pressure (pore pressure ratio between 0.2 and 0.7), the slow growth stage of pore pressure (pore pressure ratio between 0.7 and 0.85), the instantaneous failure stage (pore pressure ratio between 0.85 and 0.9), and the complete liquefaction stage (pore pressure ratio between 0.9 and 1.0).

At the rapid growth stage of pore pressure, the pore pressure increases rapidly, and the growth curve is convex. At the stable growth stage of pore pressure, the pore pressure increases steadily, the growth curve of instantaneous pore pressure is thick, and the PG has a high anti-liquefaction ability. The slow growth stage of pore pressure exists only under bidirectional vibrations, the growth rate of pore pressure gradually decreases at this stage, and the specimens maintain high strength. At the instantaneous failure stage, the pore pressure increases sharply, the difference between the maximum and minimum pore pressure decreases rapidly, the PG structure is destroyed rapidly, and the liquefaction strength is significantly reduced. At the complete liquefaction stage, the pore pressure approaches consolidation confining pressure; the growth rate of pore pressure is significantly reduced; the specimens are completely liquefied; the internal structure of PG is completely destroyed; the particles move disorderly; a large amount of interparticle pore water and bound water discharge continuously, so the curves of instantaneous pore pressure thicken again.

3.2 The Development Law of Pore Pressure and Analysis of the Dynamic Stress-Strain Curves of PG Under the Same CSR Conditions

3.2.1 The Development Law of the Pore Pressure of PG Under the Same CSR Conditions

According to the general law of soil dynamics (Xie et al., 2011), higher consolidation confining pressure indicates greater corresponding burial depth, tighter interparticle connection, and stronger anti-liquefaction ability. With the increase in dynamic stress, the seismic ability increases, while the anti-liquefaction ability decreases. However, the effect of the simultaneous action of the consolidation confining pressure and the dynamic stress on the dynamic properties of PG is unclear, so this section explores the joint effect of simultaneously increasing the two on the dynamic strength of PG under the same conditions, analyzes its development law of pore pressure, and discusses the dynamic stress-strain curve.

Figure 6 shows the development curves of the pore pressure of PG under the same conditions. The test results show that when the consolidation confining pressure is low (${\mathit{\text{σ}}}_{\mathbf{0}}^{\prime }$ < 200 kPa), the liquefaction rate of PG gradually accelerates with the increase in consolidation confining pressure and dynamic stress, and the increase in dynamic stress is the dominant factor of PG liquefaction; when the consolidation confining pressure is high (${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ > 200 kPa), the liquefaction rate of PG gradually decreases with the increase in consolidation confining pressure and dynamic stress, and the increase in consolidation confining pressure is the dominant factor of PG liquefaction; when ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 200 kPa and ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ = 100 k Pa, the liquefaction rate of PG is the fastest, and the cycle number is about 270 times.

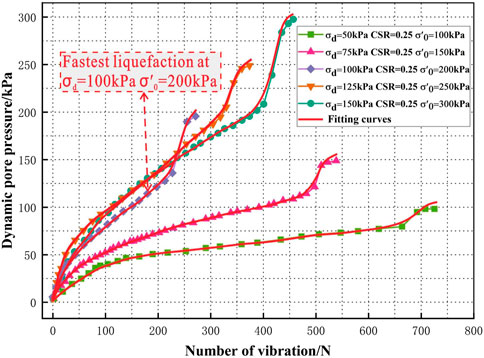
FIGURE 6. Development curves of accumulated pore pressure under unidirectional vibrations with the same CSR conditions.

When the confining pressure is low, with the rise of the confining pressure, some of the pore water and bound water in the PG skeleton seep out in a large amount (Shen et al., 2008), and some of the interparticle contact point lattices distort and deform, leading to smaller growth of the anti-liquefaction ability of PG with the increase in the confining pressure. Because PG has the property of being slightly soluble in water, some water channels form inside the specimens at the saturation stage (Zhang et al., 2007). At small amplitudes, some particles gradually move to the water channels. However, the water channels are not completely closed, and the particles gradually disorder and tend to be unstable under the vibration load. Therefore, at this stage, dynamic stress is the dominant factor of specimen liquefaction, and the dynamic strength gradually decreases with the growth of confining pressure and dynamic stress.

When the confining pressure is high, most of the pore water and bound water in PG have been discharged. With the increase in confining pressure, the interparticle connection tends to close, and PG stability gradually increases, so the increase in confining pressure enhances the anti-liquefaction ability of PG. At large amplitudes, most particles quickly move to and block the internal pores and water channels of PG to stabilize the sample structure. Therefore, at this stage, the consolidation confining pressure is the dominant factor of specimen liquefaction, and the dynamic strength gradually increases with the growth of confining pressure and dynamic stress.

When confining pressure is low, some of the pore water and bound water in the PG skeleton seep out in a large amount; near ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 200 kPa when the pore water and bound water began to drain completely; when ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ > 200 kPa, with the confining pressure continuing to increase, the particles gradually become dense and stabilized, so near ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 200 kPa when the PG reached the critical confining pressure. Similarly, near ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ = 100 kPa, the water channels gradually closed, so near ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ = 100 kPa PG reached the critical dynamic stress. Therefore, under the conditions of ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 200 kPa and ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ = 100 kPa, there is a critical phenomenon of PG liquefaction rate, and the liquefaction rate reaches the fastest at this time.

If we continue to increase the consolidation confining pressure and dynamic stress (${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 600 kPa, ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ = 300 kPa), the number of cycles required for liquefaction can reach 1,070 times, as shown in Table 2, indicating that the interparticle connection of PG tends to be tightened under high confining pressure, and the dynamic strength increases if we continue to increase the confining pressure and dynamic stress under the same CSR conditions.

3.2.2 The Analysis of Dynamic Stress–Strain Hysteresis Curves

Comparing the dynamic stress-strain curves of PG under different conditions in Figure 7, we can find that PG is axially compressed under cyclic loading. With the increase in the number of cycles, the centers of the curves keep moving in the direction of axial compression, producing plastic damage, and reflecting the deformation accumulation characteristics of PG to cyclic loading. Under cyclic loading, PG strain steadily increases after reaching the initial effective stress, showing cyclic activity. After the structural damage, the dynamic stress that the specimens can withstand decreases and converges to a constant value (Figure 7C). Before the structural damage of PG specimens, the axial strain hardly changes, indicating that the PG has high strength before the structural damage, but with the continuous application of cyclic loading, the PG structure is damaged, and the deformation increases rapidly.

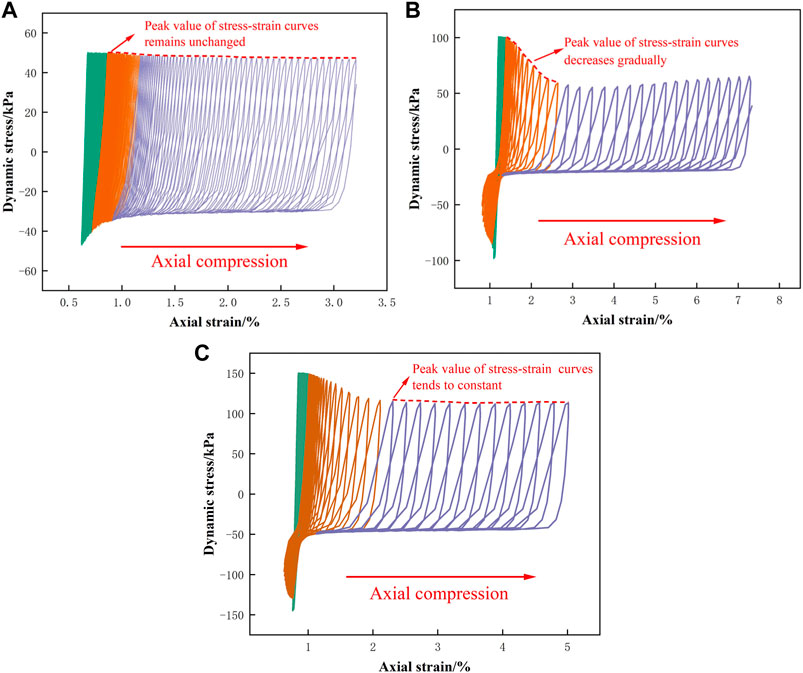
FIGURE 7. Dynamic stress–strain curves under different stress conditions with the same CSR. (A) ${\text{σ}}_0^{,}$ = 100 kPa, CSR = 0.25, ${\text{σ}}_{\text{d}}$ = 50 kPa; (B) ${\text{σ}}_0^{,}$ = 200 kPa, CSR = 0.25, ${\text{σ}}_{\text{d}}$ = 100 kPa; (C) ${\text{σ}}_0^{,}$ = 300 kPa, CSR = 0.25, ${\text{σ}}_{\text{d}}$ = 150 kPa.

Under the same CSR conditions, when the confining pressure is low (${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ < 200 kPa), the dynamic stress applied to the PG is small, and the pore pressure grows slowly to the consolidation confining pressure to complete liquefaction, at which time the peak value of the dynamic stress-strain hysteresis curve remains unchanged, and the specimens still have a large load-bearing capacity (Figure 7A). When the confining pressure is high (${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ > 200 kPa), with the increase in dynamic stress, the growth rate of pore pressure gradually accelerates, the structures of the specimens are damaged after liquefaction, and the cyclic loading-bearing capacity reduces (Figure 7B). At this time, the peak values of the dynamic stress-strain hysteresis curves decrease. In addition, the density of the hysteresis curves reflects the dynamic strength of the specimens to a certain extent. Under the same CSR conditions, the hysteresis curve when ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 100 kPa is denser than that when ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 200 kPa and ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 300 kPa, indicating that PG has higher strength when ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 100 kPa. This conclusion is verified in the aforementioned pore pressure law.

3.3 Comparison of Pore Pressure Development and Study of the Growth Model of PG Under Unidirectional and Bidirectional Vibrations With Different CSR Conditions

3.3.1 The Development Law of the Pore Pressure of PG With Unidirectional and Bidirectional Vibrations Under Different CSR Conditions

As shown in Figure 8, under the same consolidation confining pressure, the development laws of accumulated pore pressure under unidirectional and bidirectional vibrations are roughly the same. The liquefaction rate of PG gradually accelerates with the increase in CSR, and the number of vibrations required for liquefaction by bidirectional vibrations (Figure 8B) is much larger than that by unidirectional vibrations (Figure 8A). When CSR = 0.45, the specimens are cycled 36 times under unidirectional vibrations to complete liquefaction, while they are cycled more than 1,220 times under bidirectional vibrations to complete liquefaction.

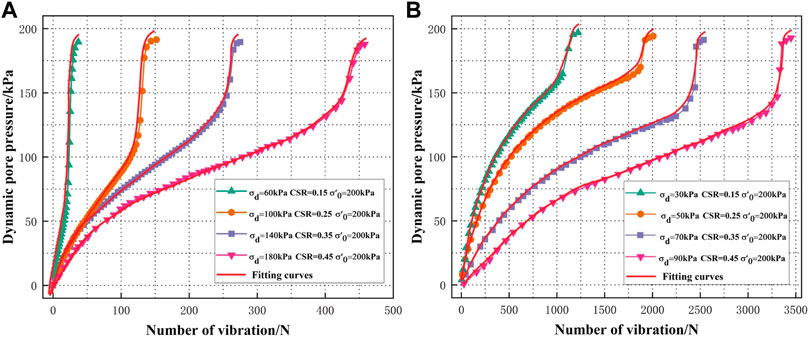
FIGURE 8. Development curves of accumulated pore pressure of PG under different vibration conditions: (A) unidirectional vibrations condition; (B) bidirectional vibrations condition.

3.3.2 BiDoseResp Pore Pressure Growth Model of PG

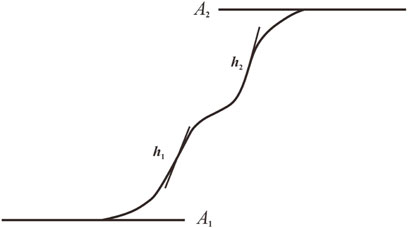
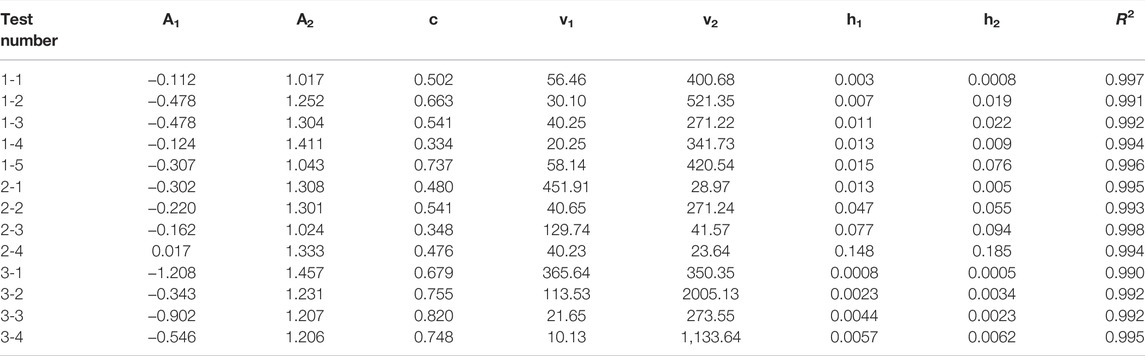
Previous scholars have proposed corresponding pore pressure growth models, such as the inverse sine trigonometric function model proposed by Seed et al. (1966) and the growth model of dynamic pore water pressure applicable to tailings materials proposed by Zhang et al. (2006) based on seed. However, the aforementioned pore pressure growth models can only describe the growth curves of dynamic pore pressure at stages in which a small amount of accumulated pore pressure grows, which are not applicable to the multi-stage accumulated dynamic pore pressure of PG. Combining the test results and the curve characteristics at each stage and citing the BiDoseResp function of the dynamic pore pressure growth model (Du et al., 2016) of tailings silt (as shown in Figure 9 and Eq. 2), we found that the characteristics at each stage of PG pore pressure growth were consistent with the h₁-A₂ section curve in the BiDoseResp function:

where A₁, A₂, c, v₁, v₂, h₁, and h₂ are model parameters; A₁ and A₂ are the range of the model; h₁ is the slope of the pore pressure curve at the rapid growth stage; and h₂ is the slope of the curve at the instantaneous failure stage. The fitted curves are shown in Figures 6 and 8. The BiDoseResp function is used to fit the curves of PG pore pressure ratio versus vibrations under unidirectional and bidirectional vibrations, and the fitting effect is good. The specific fitting parameters are shown in Table 3. The fitting results in Table 3 indicate that the slopes of the curves at the rapid growth stage and the instantaneous failure stage under unidirectional and bidirectional vibrations increase with the increase in CSR, and the growth rates of pore pressure at the rapid growth stage and the instantaneous failure stage under unidirectional vibrations are greater than those under bidirectional vibrations. In addition, the fluctuation range of parameters v₁ and v₂ is large, and the fluctuation range of the remaining parameters is relatively small. The fitting degree is more than 0.990. Therefore, it can be considered that the model has good applicability to the development law of the accumulated pore pressure of saturated PG under unidirectional and bidirectional vibrations.

FIGURE 9. BiDoseResp function characteristics.

TABLE 3. Fitting results of model parameters.

3.4 Softening Phenomenon of PG Under Bidirectional Vibrations

While the pore water pressure rises under cyclic loading, the strength of PG softens. To ensure the safety and stability of PG dams under seismic action, it is important to study the strength softening law of PG under cyclic loading. By conducting unidirectional and bidirectional vibration tests on PG under the same CSR conditions, we found that PG had a significant strain-softening phenomenon after liquefaction by bidirectional vibration (Figure 10). Numerous scholars have studied the cyclic softening of soil: Idriss et al. (1978) firstly proposed the softening index. Considering the effect of initial consolidation confining pressure, Wang et al. (2009) redefined the softening index δ as (Eq. 3):

where ${\mathit{\text{q}}}_{\mathit{\text{max}}}$ and ${\mathit{\text{q}}}_{\mathit{\text{min}}}$ are the maximum and minimum deviatoric stress of the soil sample in each cycle; ${\mathit{\text{ε}}}_{\mathbf{1},\mathit{\text{max}}}$ and ${\mathit{\text{ε}}}_{\mathbf{1},\mathit{\text{min}}}$ are the maximum and minimum axial strains in the first cycle; and ${\mathit{\text{ε}}}_{\mathit{\text{N}},\mathit{\text{max}}}$ and ${\mathit{\text{ε}}}_{\mathit{\text{N}},\mathit{\text{min}}}$ are the maximum and minimum axial strains in the Nth cycle, respectively.

FIGURE 10. Softening phenomenon of PG after liquefaction by bidirectional vibrations.

From the development curves of the softening index δ in Figure 11, it can be observed that:

1) With the increase in cyclic vibration times, the softening indexes of PG under unidirectional and bidirectional vibrations are gradually reduced. Under the same consolidation confining pressure, larger CSR suggests a faster decrease in the softening index and a higher softening degree. The softening index curves of PG under unidirectional and bidirectional vibrations have the same decreasing trends. When the softening index decreases to about 0.3 at the later liquefaction stage, the softening index of PG decreases rapidly under both unidirectional and bidirectional vibrations, and the softening of PG is accelerated, corresponding to the instantaneous failure stage. When the softening index decreases to about 0.2, the softening index decreases slowly to the minimum, corresponding to the complete liquefaction stage. The decreasing rate of PG softening indexes during liquefaction is positively correlated with the growth rate of pore pressure, indicating that the strength softening of PG is mainly caused by the growth of dynamic pore pressure, which leads to the structural damage of the specimens.

2) Under the same CSR conditions, the number of vibrations required for liquefaction of PG by bidirectional vibrations is significantly higher than that by unidirectional vibrations, but the softening index of liquefaction by bidirectional vibrations is slightly lower than that by unidirectional vibrations, indicating that the structural damage of PG is more adequate under bidirectional vibrations, the integrity of the specimens is significantly reduced after liquefaction, and PG has significant strain-softening characteristics and presents certain mobility.

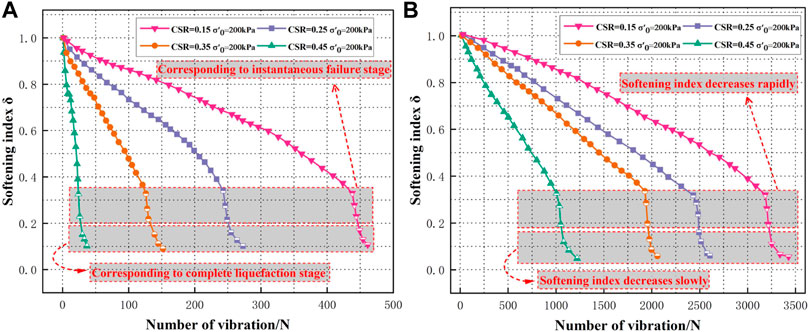
FIGURE 11. Effect of different CSR on softening index of PG under different vibration condition: (A) unidirectional vibrations condition; (B) bidirectional vibrations condition.

4 Conclusion

In this article, through the dynamic triaxial tests of PG under different consolidation and vibration conditions. The main conclusions are as follows:

1) The development curve of instantaneous pore pressure of PG under unidirectional vibrations can be divided into the rapid growth stage of pore pressure, the stable growth stage of pore pressure, the instantaneous failure stage, and the complete liquefaction stage. Under bidirectional vibrations, it can be divided into the rapid growth stage of pore pressure, the stable growth stage of pore pressure, the slow growth stage of pore pressure, the instantaneous failure stage, and the complete liquefaction stage.

2) The joint effect of consolidation confining pressure and dynamic stress on PG was explored. Due to the special consolidation and physical properties of PG, the liquefaction strength does not increase monotonically with the increase in dynamic stress and consolidation confining pressure under unidirectional vibrations with CSR = 0.25. However, there is a critical point when ${\mathit{\text{σ}}}_{\mathbf{0}}^{,}$ = 200 kPa and ${\mathit{\text{σ}}}_{\mathit{\text{d}}}$ = 100 kPa, and under this condition, the liquefaction rate of PG reaches the highest.

3) The comparison tests of unidirectional and bidirectional vibrations of PG under the same CSR conditions show that the number of vibrations required for liquefaction of PG under bidirectional vibrations is much larger than that under unidirectional vibrations, the increasing trends of accumulated pore pressure are roughly the same, and the development curves of accumulated pore pressure under both the vibrations can be fitted by BiDoseResp function model with good consistency.

4) After liquefaction by bidirectional vibrations, the structure of PG is completely destroyed, and PG is significantly softened and presents certain flow characteristics. The research results have certain reference significance for the seismic design of PG dams.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization: FK, GW, and WL; methodology: FK, and GW; formal analysis and investigation: FK, XL, and WZ; validation: FK and ZD; writing—review and editing: FK, GW, WL, and MW.

Funding

The research work was funded by the National Natural Science Foundation of China (No. 52174114), and the open fund project of the National Engineering and Technology Research Center for Development & Utilization of Phosphate Resources(No. NECP2022-07).

Conflict of Interest

Author WL is employed by China nonferrous metals industry Kunming survey and design research institute Co.LTD. Author MW is employed by National Engineering Research Center for Development and Utilization of Phosphorus Resources, Yunnan phosphate group Co. LTD.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References